О раскраске планарных графов
Теорема о пяти красках, Теорема Хивуда : Всякий связный планарный граф G можно правильно раскрасить не более чем 5-ю красками. Доказательство : Индукцией по числу p вершин графа. Вершину v можно раскрасить любой из оставшейся красок. Пусть теперь вершины v 1 , v 2 ,…,v 5 окрашены в 5 цветов C 1 , C 2 ,…,C 5 соответственно.


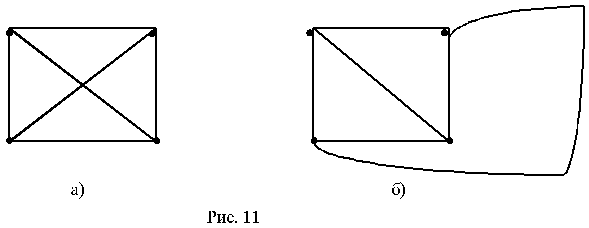
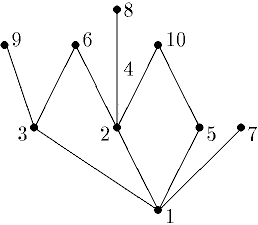

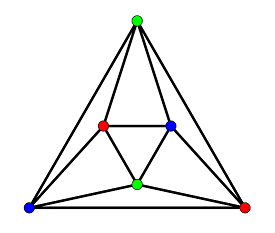

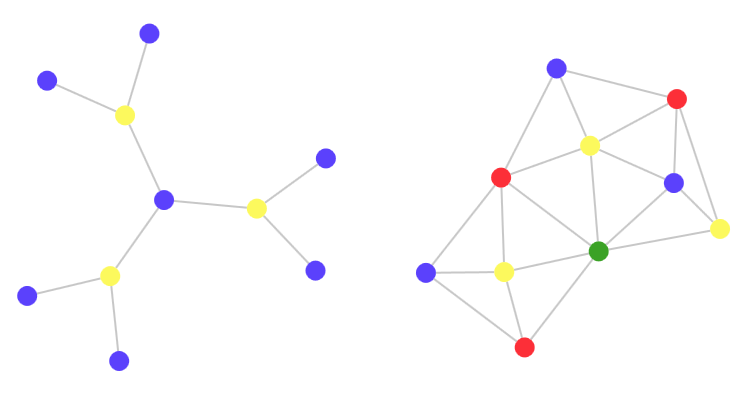
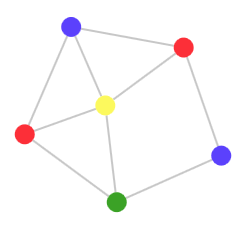
Раскрашивать можно как ребра графа, так и вершины. Коснемся сначала задачи о раскраске вершин,. Раскрасить вершины графа так, чтобы любые две смежные вершины были раскрашены в разные цветы, при этом число использованных цветов должно быть наименьшим.
- Для продолжения работы вам необходимо ввести капчу
- Напомним ее постановку. Пусть дана географическая карта страны, в которой имеется несколько областей.
- При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин.
- При изготовлении карт в целях различения отдельных областей необходимо их раскрашивать таким образом, чтобы никакие две смежные области не были раскрашены одинаково. Эта задача правильной раскраски областей планарного графа равносильна задаче правильной раскраски вершин двойственного графа.
- Материал из Викиконспекты.
- Поиск Написать публикацию. Время на прочтение 5 мин.
- Теорема о четырёх красках утверждает, что всякую расположенную на плоскости или на сфере карту можно раскрасить не более чем четырьмя разными цветами красками так, чтобы любые две области с общим участком границы имели разный цвет.
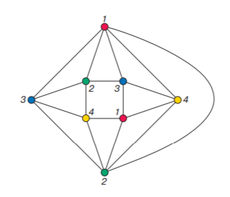

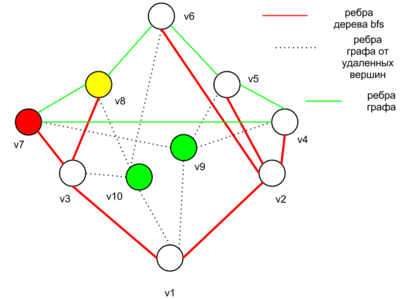



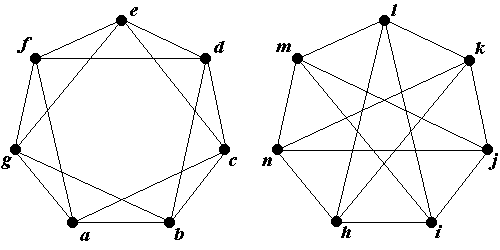
Теорема о пяти красках — ослабленный вариант теоремы о четырёх красках : вершины любого планарного графа можно покрасить в пять цветов так, чтобы любые две смежные вершины были разных цветов данный способ покраски в математике называют правильным , или, что то же самое, хроматическое число планарного графа не больше 5. Теорема была доказана Перси Хивудом в году, его доказательство основано на исправлении ошибки в неудачной попытке доказательства Альфреда Кемпе [en] предпринятой в году, которое считалось обоснованным в течение 11 лет. В отличие от теоремы о четырёх красках, доказательство является достаточно компактным. Ведётся индукцией по количеству вершин графа. Далее рассматривается два случая:.
.png)